Fuzzing Python for Correctness: Checking on ChatGPT

One of the biggest issues with LLM-generated code is a lack of trust, mostly stemming from a lack of understanding from not having written it personally, which leads to reduced confidence that the code handles edge cases properly.

What if I told you one technique would both find bugs in code (AI-generated or otherwise), as well as make you a better programmer through your ability to apply powerful testing concepts?

That technique is fuzzing for correctness, primarily accomplished through property-based testing and differential fuzzing.

It might sound fancy, but the code and process is pretty straightforward, all it takes is a bit of thinking… be warned though, it will take you to the weirdest edges of your program’s behavior (as we’ll see).

This is part 2 in a series on fuzzing Python code, so let’s start by quickly recapping part 1.

Where we left off

#

We started by writing a basic fuzz harness using Atheris that generates randomized inputs and feeds them through the target function very quickly, catching any unexpected exceptions and stopping and saving off the faulting input.

The bulk of the harness is basically just these two functions:

def get_input(data: bytes) -> str:
    """Create an input of the right type from the data"""
    fdp = atheris.FuzzedDataProvider(data)
    max_len = 20
    return fdp.ConsumeUnicodeNoSurrogates(max_len)

def TestOneInput(data: bytes):
    """Run an input through the target function"""
    # get input
    expr = get_input(data)

    # feed input to target
    try:
        result = evaluate_expression(expr)
        assert isinstance(result, float)
    except ValueError:
        pass
    except ZeroDivisionError:
        pass

Testing with a harness like this makes finding, reproducing, and fixing unhandled exceptions much easier and faster! Feel free to refer back to that post if you want a refresher on how to run such a harness or interpret the output.

Our example target was a function that evaluates arithmetic expressions, an example of a non-trivial task you might see in an undergrad class… so naturally I asked an LLM to write it.

But we haven’t looked at or talked about the code of our target yet, other than its interface.

This was on purpose, to show:

1. Writing a test harness is largely agnostic of the target implementation
2. We shouldn’t rely only our ability to read code to assess correctness

In fact, I’d say that reading generated code can be a crutch, since it offers a false sense of security. This is because we humans suffer from confirmation bias and want to assume the code is correct, rather than meticulously working through all the details.

So we know the target function is supposed to handle arithmetic expressions… but so far all the fuzzing confirms is that it only throws two kinds of exceptions and returns the correct type (when it isn’t throwing exceptions).

Now it’s time to figure out if this code is actually working correctly!

Correctness start with a specification

#

To define what is “correct”, we first need to make it explicitly clear what is allowed and what is not, in other words, a specification.

In a perfect world, a correct program should do exactly what is stated in the specification and nothing else.

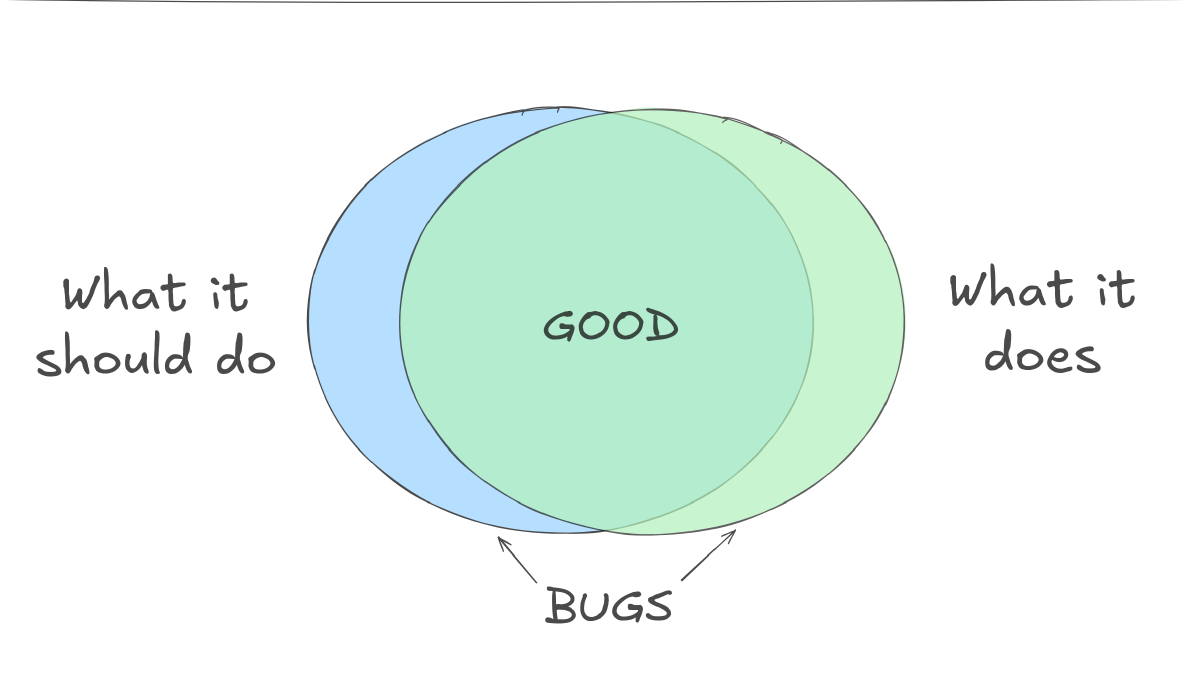
In reality, I think of every real-world program as a Venn diagram with the two parts being the specification (what it should do) and the implementation (what the program actually does).

Ideally there’s a perfect overlap between the implementation and the spec, because anything else is either incorrect or unexpected behavior (bugs or “features”, depending on framing).

Writing a good specification is a challenge, because both ambiguity and omissions can lead to problems.

So for our example of a basic arithmetic calculator, what was the spec for that? We described it as a function that evaluates an arithmetic expression, but the prompt we gave to the LLM was:

Write a Python function that takes a mathematical expression as a string
evaluates it.  The function should handle basic arithmetic operators and
precedence but does not need to handle parentheses.

This still leaves a lot of potential questions:

• Are negative numbers supported?
• Are arbitrary floats supported as inputs?
• Should parentheses be considered an error?
• What is the correct thing to do when given an invalid input?
• Are common float concepts such as NaN and infinity supported?

The answers to these questions require understanding context and intent, which is often lacking when using prompts to generate code.

So one of the best reasons to write a spec for generated code is to make sure they didn’t sneak any weird assumptions in.

Good news though!

The process of developing a harness to fuzz for correctness doesn’t require us to have the full spec in our head before we start. The steps will help us think on specific requirements, as well as sometimes surfacing assumptions and requirements.

Basically, we’ll be incrementally increasing the functionality of the test harness and getting specific counterexamples, testing our requirements and improving the code as we go.

Fuzzing for correctness: Property-Based Testing

#

Testing for correctness is a big deal when fuzzing Python code, because much of the value is from gaining confidence the code does what it’s supposed to.

This is a contrast to non-memory-safe languages, where a significant value is gained just knowing weird inputs aren’t causing memory corruption.

“Property-Based testing” is basically just taking the properties that define correctness for our target, and turning those into assertions.

This is a simple idea, but assertions in a fuzz harness are extra powerful because fuzzing literally comes up with millions of inputs and stops to tell you if any of them trigger the assert.

So what’s an example of a property?

The textbook example is to consider sorting algorithms, where there are three obvious properties that describe if a sorting algorithm is working.

1. Length: Input and output lengths should match
2. Contents: Only the order of the contents should vary
3. Order: The contents of the output should be in order

Testing these properties on number sorting is pretty straightforward in Python:

def TestOneInput(data: bytes):

    in_list = get_input(data)

    out_list = target_sort_function(in_list)

    # Property: size
    assert len(in_list) == len(out_list), "Size must match"

    # Property: contents
    input_copy = in_list[:]
    for n in out_list:
        assert n in input_copy
        input_copy.remove(n)
    assert len(input_copy) == 0, "Contents must match"

    # Property: order
    for i in range(len(out_list)-1):
        assert out_list[i] <= out_list[i+1], "List must be sorted"

We know that if any of those assertions fire, the sorting algorithm has a bug. Conversely, if an algorithm can pass these tests on millions of inputs, it’s probably correct (barring a backdoor bug), at least for whatever kinds of input get_input creates.

Another common property test that’s easy to check is whether encode/decode pairs round-trip correctly. Typically encode/decode functions have the property that if you run both functions in turn, you should get back what you put in:

out_data = decode(encode(in_data))
assert in_data == out_data, "Encode/Decode did not round trip properly!"

For our running example of an arithmetic expression evaluator, the most obvious property might be that output should be mathematically correct. While obvious, this isn’t the easiest thing to test.. so what other properties could we check first?

Let’s start by looking at what exceptions we know are thrown. A calculator shouldn’t just throw ValueErrors whenever it feels like it, it should have specific reasons (and ideally describe them in the exception).

Let’s take our harness from the first post and modify it to print out the ValueError exceptions along with the input that caused them instead of silently passing.

def TestOneInput(data: bytes) -> None:

    expr = get_input(data)

    try:
        result = evaluate_expression(expr)
        assert isinstance(result, float)
    except ValueError as e:
        print(f"ValueError: {expr=}, {e=}")  # Show us the reason
    except ZeroDivisionError as e:
        pass

Running the harness now will print a lot of errors really fast, so we can just CTRL+C out and peruse them.

The most common ValueError observed is about invalid characters (our function can accept arbitrary Unicode strings after all), so let’s define a property that an input must consist of valid characters only:

def contains_bad_characters(expr: str) -> bool:
    """Property test: expressions are only numbers, spaces, and operators"""

    for c in expr:
        if (c in '012456789. +-*/') is False:
            return True

    return False

But to fully check this property, we actually need to test both sides: when ValueErrors are thrown and when they aren’t.

def TestOneInput(data: bytes) -> None:
    """Run an input through the target function"""

    expr = get_input(data)

    bad_chars = contains_bad_characters(expr)

    try:
        result = evaluate_expression(expr)

        assert isinstance(result, float)  # type check

        # If this property is true, we should have thrown
        if bad_chars is True:
            raise Exception(
                'Should have thrown a ValueError due to bad characters: ' +
                f'{expr=}, {result=}'
            )

    except ValueError as exception:
        # If this property is True, this is an expected ValueError
        if bad_chars is True:
            pass
        # Else it's an unexpected ValueError; stop so we can add properties
        else:
            raise Exception(
                'Threw an exception for unexpected reasons: ' +
                f'{expr=}, {exception=}'
            )

    except ZeroDivisionError as e:
        pass

This gives us a positive and negative test for this property of our expression evaluator spec.

This design of throwing unhandled exceptions means that fuzzing will stop as soon as we find an input that triggers them.

This is nice because the fuzzer saves the input, which we can test against until the behavior is handled properly. But we can also re-run the fuzzer and get multiple crashes to see if it’s always the same exact input or if there’s a “cluster” of inputs that describe a larger issue.

If we repeat this process, generating inputs that cause exceptions and looking at why that’s happening, we’ll see a few common cases for ValueErrors being thrown that we can add properties for:

1. The input is empty
2. The input is non-ascii Unicode that gets evaluated despite failing the bad_characters check
3. The input is not a valid expression (e.g. 1++1 or *0 )

The first one is easy, so we won’t cover it. The second case is weirder, but is a good example of how fuzzing helps us find corner cases (especially when it comes to raw bytes):

I jumped into a debugger to figure out what was going on here, and found that the target implementation used isdigit, which was allowing Unicode characters that apparently are considered digits.

So I changed the bad_chars check to use the isdigit function to handle Unicode digits… and then promptly discovered that there are some strings that consist of a character where isdigit returns True, but Python cannot convert the string to a float (example '¹').

This level of tomfoolery should really make you question whether you really need to support Unicode and all of its weird corners.

Testing non-trivial properties

#

But the third property we mentioned (“the input is not a valid expression”) is a bit trickier, because to do it right we have to parse the expression ourselves. It’s doable, but it means re-implementing part of what we’re testing, and of course whatever check we write has to be correct.

If you find yourself starting to re-implement non-trivial functionality, stop and ask two things:

First, could you use differential testing (which we’ll cover in the next section)?

Second, do you really care about correctness bugs in this code? Because writing such checks takes effort and you aren’t guaranteed to find anything interesting… but it does give us an opportunity to get to the edges of behavior where some really weird bugs live.

Obviously I wrote a malformed expression check for the purposes of this post, basically ensuring that operators had numbers on both sides, which took around 50 lines of code since it had to handle negatives, floats, and spaces properly.

And it found a bug I would never have expected:

The LLM-generated expression evaluator code I was testing allowed expressions in postfix and prefix notation, often known as Reverse Polish Notation (RPN). This means that in addition to standard infix notation expressions like "9 / 3", expressions like "/ 9 3" or "9 3 /" would also be evaluated.

This was a complete surprise to me, and in my mind this is a most definitely bug and not a feature.

If you’re wondering how this could happen, it’s because the implementation attempted to parse expressions to RPN in order to evaluate them, but the parsing code didn’t properly enforce ordering. While this approach is reasonable, the implementation is simply incorrect.

Overall, this was an fantastic example of something that is not easy to spot with manual review, and not something that a programmer is likely to write a unit test for.

At this point we could fix these issues with the implementation, but since the code was autogenerated, we’re going to skip that and move on to the next technique.

Differential fuzzing: side-by-side correctness check

#

So remember how earlier I mentioned that checking the math is done correctly an obvious but non-trivial property to check?

Now it’s time to do the math!

Differential fuzzing is a really simple idea: if there are other implementations of what we’re writing, we can just check against their results to see if our implementation agrees.

This is a really powerful idea and is excellent for complex algorithms that would be difficult to spot issues in, like encryption schemes or compilers.

The only thing it requires is that you have an alternative implementation that has exactly the same specification as what you wrote. Any differences in spec will need to be handled by your harness, which we’d prefer to avoid.

For our example, we could look for other things that evaluate basic arithmetic expressions with operator precedence. Like the built-in eval function!

As mentioned, you have to test against something that has the same spec. On my machine eval does not try to evaluate weird Unicode strings as equations, so the first adjustment was to change our input generation function to just build a string from the valid characters.

def get_input(data: bytes) -> str:
    """Create an input of the right type from the data"""
    fdp = atheris.FuzzedDataProvider(data)

    max_len = 20
    # Conservative: Don't try to make strings longer than the input
    effective_len = min(len(data), max_len)

    ALLOWED_CHARACTERS = list(string.digits + '.' + ' ' + '+-*/')

    output = ''
    for _ in range(effective_len):
        output += fdp.PickValueInList(ALLOWED_CHARACTERS)

    return output

Otherwise it’s pretty straightforward to add a check that calls eval on any expression that yields a valid result and then compare the two results.

def TestOneInput(data: bytes) -> None:
    """Run an input through the target function"""

    expr = get_input(data)

    # Correctness properties around well-formed expressions
    is_empty = expr == ''
    bad_expr = is_malformed_expression(expr)

    try:
        # Send to target function
        result = evaluate_expression(expr)

        # ...Removed for clarity...

        # Correctness check: do our results match?
        eval_result = eval(expr)
        if result != eval_result:
            raise Exception(
                f'Math mismatch for {expr=}: {result=} vs {eval_result=}'
            )

Add this code and you’ll come face to face with our first example of annoyances caused by small differences in the spec between our implementation and the other.

eval doesn’t allow leading zeroes, but our code under test does. Seems a bit picky to me, but we can either make our code similarly picky or filter leading zeroes before feeding the inputs to eval.

I chose the latter.

Run it with such a filter, and we’ll find that differential fuzzing also exposes the bug we found earlier:

Naturally eval does not allow expressions in postfix or prefix notation.

This bug is quickly reached, so if we re-run the fuzzer a bunch that’s probably all we’ll see. But if we catch and ignore the SyntaxErrors that eval throws, and just look for math errors, what do we find?

We find that there is a tiny difference of floats (and apparently scientific notation) between the two implementations that causes our equality check to fail.

The bizarro part is that both values are floats, not strings, so while the difference appears to be zero, a basic equality check does not suffice:

While this isn’t a bug, it is illustrative of how we’ve discovered some of the outer reaches of our target code’s behavior, more than we’d even be able to discover with a very thorough reading.

Fuzzing even longer after adding this check, we will eventually find examples where the differences in float arithmetic are measurable, but tiny (either in absolute or relative terms).

So we added a final check to set a reasonable threshold for floating point error and… no problems found.

With >25K execs/sec for longer than 10 minutes of fuzzing with no new coverage, we can have pretty good confidence that there aren’t other weird math problems happening.

Time to take a step back and review.

Reflecting on differential fuzzing

#

Using eval as an alternate implementation gives us pretty strong confidence nothing was going wrong with in the math in the target expression evaluator, which is otherwise difficult to prove.

This confidence comes from knowing that we tested with millions of inputs, and we got to the point of detecting microscopic differences from floating point rounding.

But the final version of our harness also ignored the fact that the target implementation is accepting RPN expressions, which we consider flat out wrong. Luckily, other than that one bit of purposeful flexibility, the harness was primarily built to test the spec, not a particular implementation.

So in theory, this means we can swap in different implementations and test them out with minimal changes to the harness, which is kind of the point with differential fuzzing! Swapping in different implementations in this harness is as easy as changing the import statement to refer to a different file.

with atheris.instrument_imports():
    #from target.evaluate import evaluate_expression
    from target.other_implementation import evaluate_expression

Before we forget though, we need to revert the parts where we were specifically ignoring when eval was throwing syntax errors, since that is an important check.

In my testing, I tried multiple iterations of LLM-generated code, and this harness caught bugs in ALL of them in less than a second.

Frankly, the kinds of bugs from LLM-generated code were pretty sad.

But not as sad as trying to coach the LLMs into fixing said errors, which manages to both be frustrating and depressing at the same time, like talking to a wall that is supposed to be “as smart as a PhD.”

These errors were things like:

• Negative numbers weren’t supported
• Randomly returning non-float types
• Running into unexpected errors while evaluating “simple” expressions like a single number, or just an operator, or an empty string

In reality, this task is pretty difficult for current LLMs and even with careful prompting. Since that’s not our focus today, let’s finish with some notes on effectiveness.

The process of fuzzing Python for correctness

#

So what was the process we followed so far to effectively fuzz for correctness?

1. Set up the basic fuzzing harness so you’re passing an input in, testing the output type, and catching each type of exception the target throws.
2. Start implementing property testing by thinking about how to evaluate outputs as correct or incorrect, or when exceptions should be thrown
3. Change the exception handling to print out exceptions and the inputs that cause them in order to find patterns, then turn those patterns into properties
4. Add checks for properties on both the positive and negative sides of the target function logic, throwing exceptions when unexpected cases are encountered
5. Continue until you have checks that define most (or all) of the reasons an implementation could be considered correct

This take some time, but it can lead to very robust testing in a fairly step-by-step manner, so is worth it for code that requires additional scrutiny.

One important thing to note was some of our changes affected the expectations of the fuzzer, like changing inputs from Unicode to only allowed characters. But changing expectations doesn’t change the requirements for the code under test.

If the target can receive Unicode, it should probably be tested with Unicode so we know what will happen in the weird cases.

A second thing to note is that a lot of what we did slowed down our fuzzing. The harness we started with got ~70K execs/sec in my VM (but catching no real bugs), while the final one measured around ~25K.

The speed of your fuzzer is critical to its effectiveness, because fuzzers’ primary value is that they can try millions of inputs. This doesn’t mean we should remove property testing or slightly involved checks, we just have to understand what we’re testing and keep an eye on speed.

Another thing to consider about effectiveness is how much of the input is getting to the heart of the target.

For example, if we’re just throwing random strings at something that has strong expectations of input structure, the vast majority of inputs will likely be discarded by the parsing layer.

If we were depict the state space for our expression evaluator, it would be something like the image below, but with much larger reductions at each step.

So while you do want to catch bugs at the parsing layer, you also want a way to efficiently test the other layers.

In this case it might be worth having a second harness that leverages FuzzedDataProvider or something similar to only generate inputs that are considered valid.

The last benefit of building out property testing is that we end up with a good approximation of a spec, which could also help make our LLM prompts more effective in generating correct code.

In my limited testing, just giving an LLM a detailed spec isn’t enough to get the current models to write code that perfectly meets the requirements, but in the future this could be a real possibility.

Until then, we have a powerful process to specify, test, and discover different properties that can help with the correctness of our code

Increased confidence with fuzzing

#

So today we showed how to implement two important concepts in fuzzing for correctness, Property-based testing and differential fuzzing.

We also demonstrated a step-by-step process to gradually improve our harness, find some weird bugs, and end up building out a specification.

This isn’t what I thought I’d find when I started to explore this, but it definitely turned out interesting!

If you want to stay up to date with more content at the intersection of development, security, and visualization, keep up with me on Mastodon, Twitter, or Bluesky.